数字签名技术在多个行业被广泛运用,尤其在交易领域,椭圆曲线数字加密算法ECDSA扮演着极其重要的角色。那么,这个算法是如何运作的?它又是如何执行点倍积运算的?下面,我们将对这些问题进行详细的分析。
数字签名算法应用
交易环节中,数字签名技术扮演着极其重要的角色。每当交易项目确定,便会为其实施数字签名,以此来确保交易的真实性和不可篡改性。这样的做法使得每一笔数字交易都显得更加稳固和可靠,对金融等多个行业产生了广泛而深远的影响。
ECDSA理论基础
ECDSA是数字签名算法的一种,它以椭圆曲线密码学ECC为基础。ECC的理论核心是椭圆曲线上的点倍乘。椭圆曲线对于ECDSA极为关键,与ECC相结合,构成了数字签名的全面体系。
椭圆曲线点倍积概念
计算椭圆曲线的点倍积,需将一个点在曲线上连续自加,直到达到另一个特定位置。选取椭圆曲线上的点P作为起点,点R作为终点,即可得出相应的点倍积公式。在公式中,需将标量置于点的左侧。
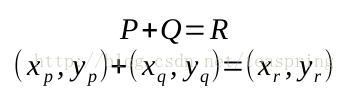
椭圆曲线方程确定
椭圆曲线的几何方程在理论上是已知的,通常通过两个标量参数a和b来描述。不同的a和b值会形成不同的图形。比如,当a和b的值分别是-7和6时,曲线会呈现出红色;而当a和b的值分别是-6和6时,曲线则会变成蓝色。
椭圆曲线点相加方法
在执行椭圆曲线上的点倍积运算之前,必须了解椭圆曲线上的点加法。以红色椭圆曲线为例,若选取两个点P和Q,它们相加会得到一个新点R。点R位于P和Q连线的延长部分,并且是这条延长线与椭圆曲线交于点T的对称点。结合XY坐标和椭圆曲线的公式,我们可以计算出点R的确切坐标。
计算椭圆曲线点倍积
知道了前面的知识,我们就能进行椭圆曲线上的点倍积运算。当需要计算Q等于d乘以P时,首先要把标量d转换成二进制形式。在编写代码时,我们会把系数以数组的形式来展示。利用“点相加”和“点翻倍”这两种方法,我们可以计算出R点的坐标,进而得到最终结果。
在进行椭圆曲线计算时,您是否遇到过点倍积运算的难题?欢迎在评论区讲述您的经历,同时别忘了点赞和分享这篇文章。


暂无评论
发表评论